Data Science Interviewing Pt. 2: Area Under the Curve Edition

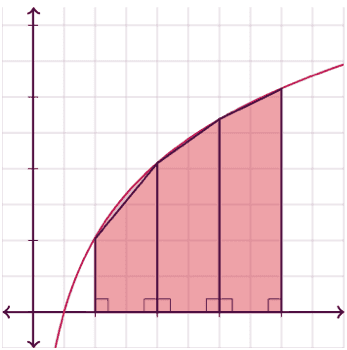
During a past interview, I was subjected to an hour take-home coding challenge in which I was asked to implement various coding exercises from scratch in my programming language of choice. In this post, I’ll provide an overview of one of the exercises from that coding challenge, which was to calculate the area under the curve given a set of points using the trapezoidal rule, and a basic implementation of it in Python.

What is the Trapezoidal Rule?

The trapezoidal rule is an integration technique used to approximate the definite integral of a function. It divides the area under a curve into a series of trapezoids and calculates the sum of their areas to estimate the integral.

How does this Relate to Data Science?

There are several potential applications of the trapezoidal rule in data science, but the one I want to focus on in this section is evaluation metrics.

Evaluation metrics like Receiver Operating Characteristic (ROC) curves and Precision-Recall (PR) curves are used to assess the performance of classification models.

ROC curves are typically used to evaluate binary classification models by illustrating the trade-off between the true positive rate (TPR) and the false positive rate (FPR). A quick refresher on TPR and FPR…

Let’s assume that you, the reader, go on a fishing trip and you only want to catch mahi-mahi.

• True Positive Rate: Measures the proportion of mahi-mahi that you successfully caught out of all of the mahi-mahi present in the ocean. TPR = True Positives / (True Positives + False Negatives)
• False Positive Rate: Measures the proportion of non-mahi-mahi that you caught that were incorrectly identified as mahi-mahi. FPR = False Positives / (False Positives + True Negatives)

ROC curves are created by plotting the TPR on the y-axis and the FPR on the x-axis at different classification thresholds. The optimal point on a ROC curve will depend on the requirements of the problem, specifically the relevant importance of maximizing true positives while minimizing false positives.

PR curves are typically used to evaluate binary classification models by illustrating the trade-off between precision and recall. Another quick refresher, but this time on precision and recall…

Let’s assume that you go on another fishing trip and you still only want to catch mahi-mahi.

• Precision: You catch 10 fish in total, and 9/10 were mahi-mahi and 1/10 was a magikarp. In this case, your precision would be high because you had a large number of true catches, the majority of the fish you caught were mahi-mahi, while you had a small number of false catches, only one non-mahi-mahi. Precision = True Positives / (True Positives + False Positives)
• Recall (also known as TPR): You catch 9 mahi-mahi, but there are thousands of mahi-mahi swimming in the ocean. In this situation, your recall would be low because you missed out on catching more of the thousands of mahi-mahi; your catch represented only a small portion of the possible mahi-mahi that were available. Recall = True Positives / (True Positives + False Negatives)

The precision-recall trade-off becomes apparent because there is a balance between being highly selective (casting a small net, but in an area where you know there are mainly mahi-mahi) and more inclusive (casting a wide net, allowing you to catch a lot of mahi-mahi, but a lot of other fish that you didn’t want, like those pesky magikarp, as well).

PR curves are generated by plotting the precision on the y-axis and the recall on the x-axis at different classification thresholds. The optimal point on a PR curve will depend on the problem. You might want to prioritize high precision at the expense of recall to avoid false items. You might want to prioritize high recall and the expense of precision to ensure you capture all of the desired items.

Looking at each curve is useful, but we need a graph-agnostic way of assessing the information provided by the curves. Area Under the Curve (AUC), which can be estimated utilizing the trapezoidal rule, is a way to quantify the performance of the curves. ROC AUC ranges from 0 to 1, where a higher AUC indicates better model performance in terms of the model’s ability to discriminate between positive and negative instances. PR AUC ranges from 0 to 1, where a higher AUC indicates better model performance in terms of the model’s ability to make accurate positive predictions and retrieve positive instances from the data.

Basic Implementation of the Trapezoidal Rule in Python

def calculate_trapezoidal_rule_area(x: List[float], y: List[float]) -> float:
    if len(x) != len(y):
        raise ValueError("x and y must be the same length")

    areas_sum = 0.0

    # Area of a trapezoid is 1/2 x
    # (sum of the lengths of the parallel sides) x
    # perpendicular distance between parallel sides
    for i in range(1, len(x)):
        y_sum = y[i] + y[i-1]
        width = x[i] - x[i-1]
        areas_sum += 0.5 * y_sum * width

    return round(areas_sum, 2)

I decided to compare my implementation to scikit-learn’s implementation since it is also calculated using the trapezoidal rule.

My implementation: 4.95

scikit-learn implementation: 4.95

Success!

Full Code

from typing import List

from sklearn import metrics


def calculate_trapezoidal_rule_area(x: List[float], y: List[float]) -> float:
    """Calculates the area under the curve using the trapezoidal rule

    Args:
        x (list or array): Array of x values
        y (list or array): Array of y values corresponding to each x value

    Returns:
        float: The estimated area under the curve

    Raises:
        ValueError: If the lengths of x and y are different
    """
    if len(x) != len(y):
        raise ValueError("x and y must be the same length")

    areas_sum = 0.0

    # Area of a trapezoid is 1/2 x
    # (sum of the lengths of the parallel sides) x
    # perpendicular distance between parallel sides
    for i in range(1, len(x)):
        y_sum = y[i] + y[i-1]
        width = x[i] - x[i-1]
        areas_sum += 0.5 * y_sum * width

    return round(areas_sum, 2)


if __name__ == "__main__":
    x = [0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 7.5, 8.0, 8.5, 9.0, 9.5]
    y = [0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 0.8, 0.6, 0.4, 0.2, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 0.8, 0.6, 0.4, 0.2]

    auc = calculate_trapezoidal_rule_area(x, y)
    print(f"My implementation: {auc}\n")

    sklearn_auc = metrics.auc(x, y)
    print(f"scikit-learn implementation: {sklearn_auc}")